Project: A little bit of Reverend Bayes all night long.
Can you predict when Lou Bega's greatest hit, Mambo No. 5, was released based on the names of all the women mentioned in the song?
Introductory ramble
Lou Bega’s iconic hit Mambo No. 5 was released in 1999 to critical and financial acclaim. Even 25 years after its release, the song appears in my regular rotation. From my recent play through, I wondered about the names that appear in the song: Angela, Pamela, Sandra, Rita, Monica, Erica, Tina, Mary, and Jessica.
I realized that none of my friends have these names. For me, I associate Sandra and Monica with women maybe twenty years my senior. “Man, when did this song come out?” I thought and I realized my big question: can you predict when Lou Bega’s greatest hit, Mambo No. 5, was released by the names of all the women that appear in the song?
Thankfully, we have a treasure trove of data and the handy Bayes formula. This is a silly project to keep ourselves sharp about Bayesian inference.
Attack plan
The full math is in my digital garden because writing math in Substack is a lesson in pain. But as a reminder, the Bayes formula for our exact situation would be:
where we are interested in the posterior distribution, or the probability of the song’s release year (Y_R) given the names (N) that appear in the song. This posterior is proportional to the likelihood or the probability of observing the names given the song’s release year multiplied by the prior distribution, which represents my best informed belief about when the song was released. I then divide by the probability of observing all names Pr(N) over all possible release years.
Let’s examine the probability of observing these names in a song from 1985, which we can estimate using the joint probability distribution of names and release years. For example, under the assumption that name occurrences are independent, the probability of observing Angela, Pamela, Sandra, Rita, Monica, Erica, Tina, Mary, and Jessica in 1985 would be the product of their individual probabilities of occurrence- which we can grab from data of popular baby girl names.
But there’s a slight hiccup with our plan! Mambo No. 5 was released in 1999, but the popular baby girl names of 1999 would not automatically tell us that the song was released that year. We need to account for the lag. Lou Bega wasn’t meeting newborn infants but was most flirting with adult women (18–35) so we should be looking at the popularity of names around 1960 and 1980.
Before we do more with the Bayesian data, let’s just check the data.
Getting the data
All those name popularity websites get their data from the official United States Social Security website. Even on the landing page, you can see that the government provides the most popular names for boys and girls:
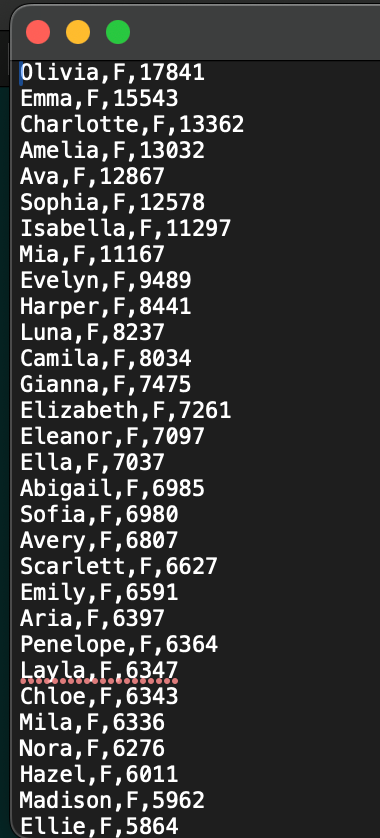
But we’re interested in the total occurrence of baby names for each year (starting from 1880) which you download as a collection of individual text files. With this wealth of information, it’s no wonder that there are a lot of interesting analyses floating online (see: How to Tell Someone’s Age When All You Know Is Her Name and Predicting names from ages). Here’s an example of what the data looks like for 2024, where the first column is the name, the sex (female/male), and the number of occurrences:
Subsetting the names to include only females, we can divide the total occurrence of a name by the total number of names given to baby girls to get the probabilities we need. So, I created a function to wrangle all of the text files into one dataframe. However, I should have realized that there’s an R package with the data already combined (Boo!).
Plotting out the data
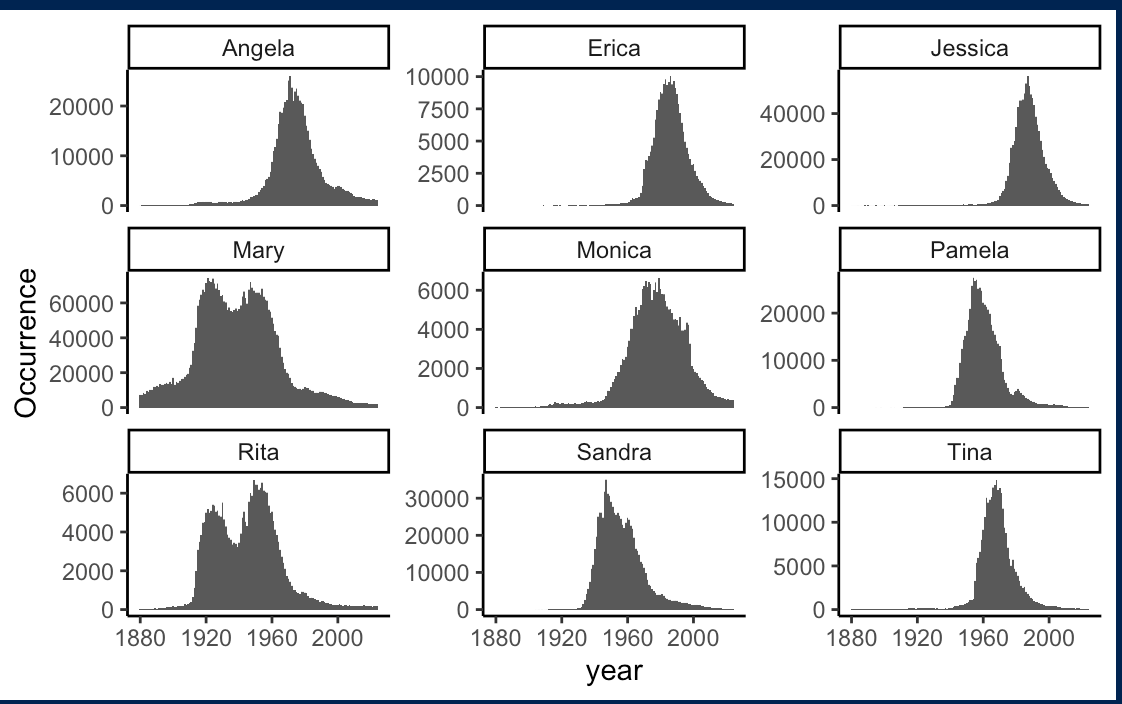
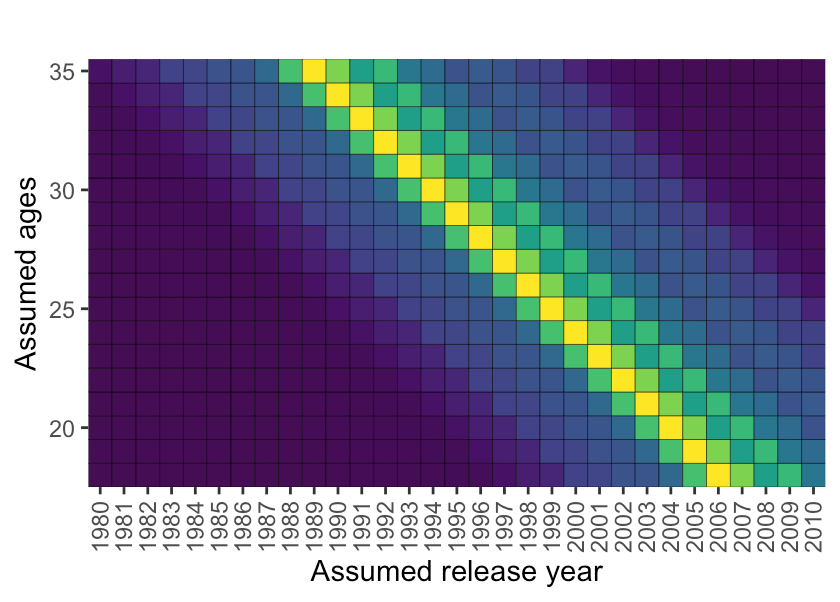
Interesting. Some names are associated with people born between 1920 and 1960 (Mary, for example). Look at Jessica; however, it was not really popular until after 1960, peaking in the 1970s. If the names were popular through the decades, it would make it quite difficult to discern the release year. Luckily, baby girl names tend to cycle—the above figures look promising, and I have some hope!
Continuing on with the Bayesian analysis
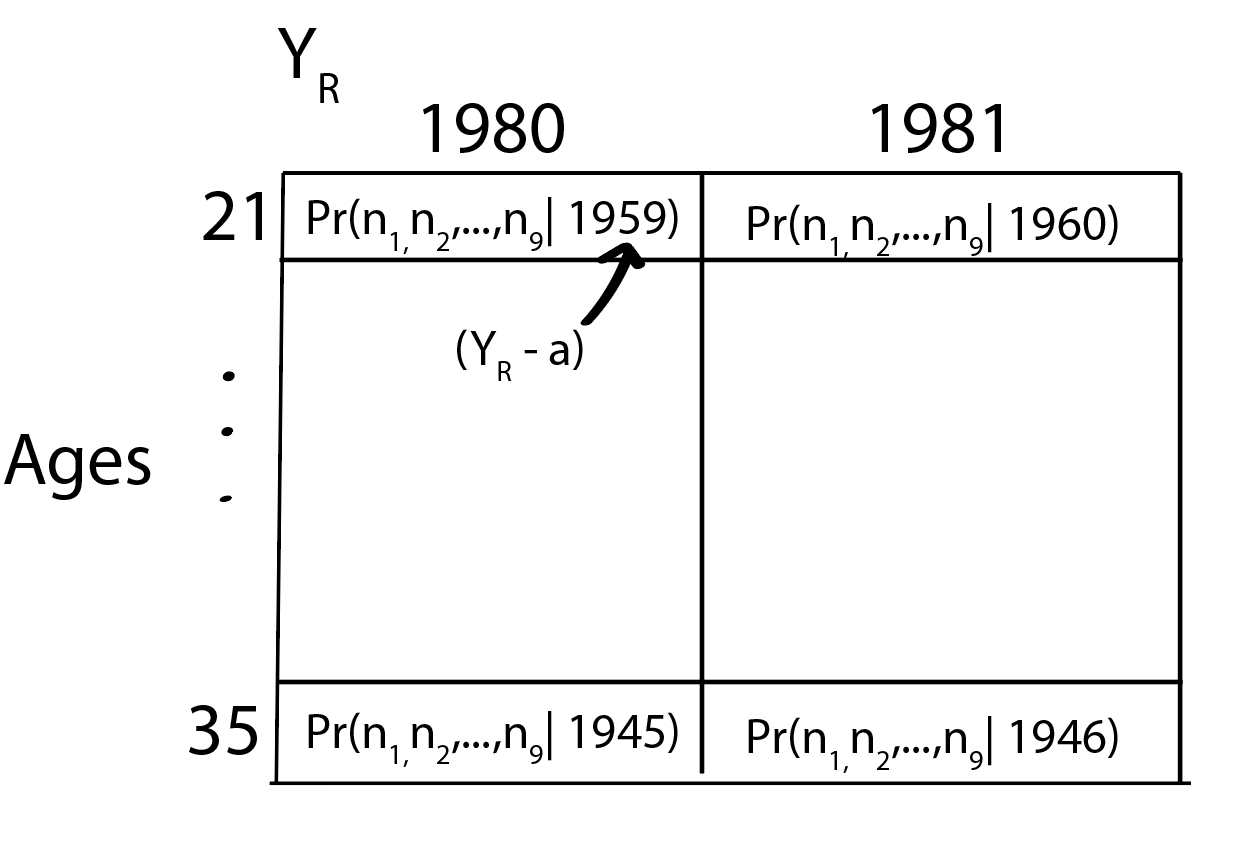
How do we account for the lag where the women name appearing in the song were chosen decades past. Well, given a range of release years AND the ages, we can back calculate to get a range of birth years:
For example, if we guess the release year is 1980 and assume that all women are 21 years old, then we would be looking at the name popularity in 1959. We can do this for release years for 1981, 1982, and so on (which would correspond to birth years of 1960, 1961, 1962, and so on). Keeping the release year fixed, we can also look across the different ages. If the song was released in 1980 and the women were instead 35, we should be looking at 1945. Imagine we’re constructing the table like below:
If you fill it out and create a pretty ggplot2.
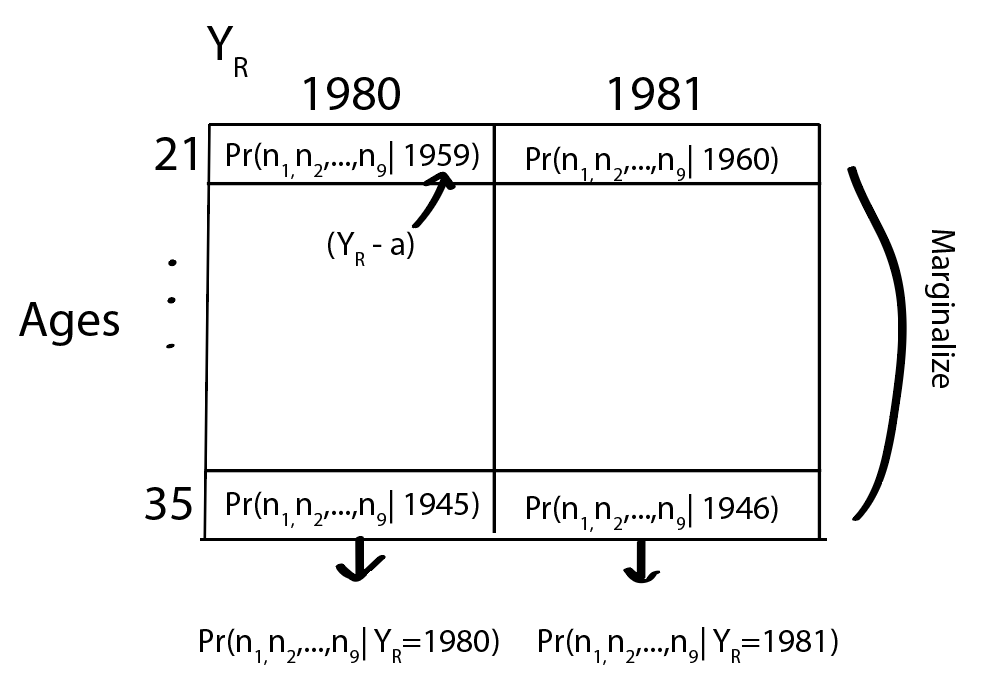
We can then marginalize over the ages (see this PDF for reference):
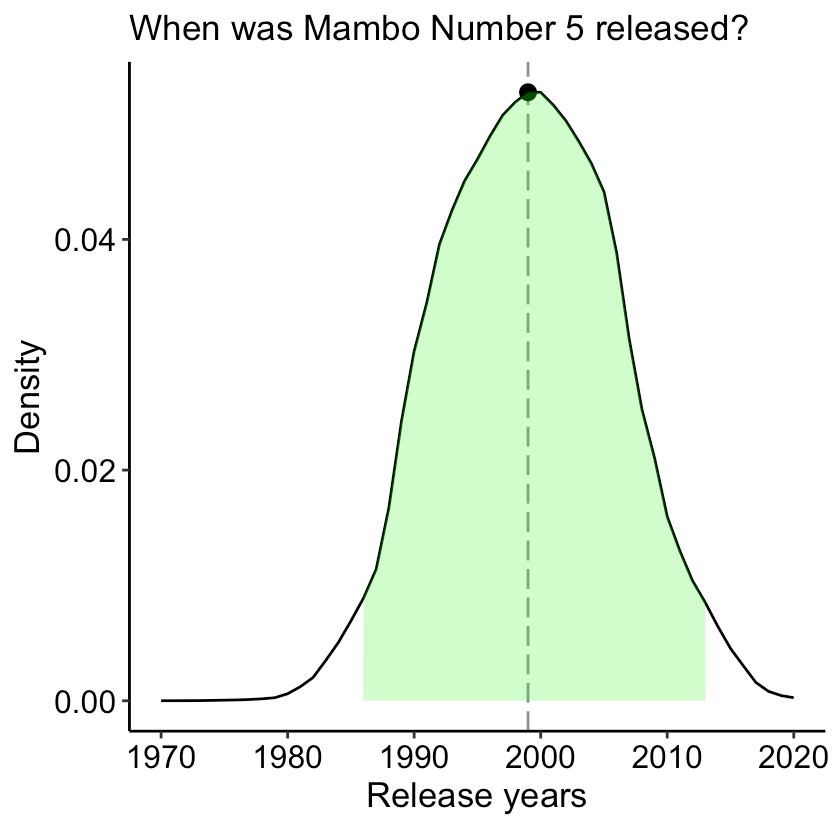
So, we now have the likelihood function, which we can multiply by our prior (which, for simplicity, I assume follows a uniform distribution ranging from 1970 to 2020). Aha! We’ve got the posterior distribution, the Maximum A Posteriori (MAP), as well as the credible interval:
Based on the MAP, the release year that maximizes our posterior distribution is 1999, with the credible interval ranging from 1986 to 2008. I feel like that’s a pretty wide interval, but this is a silly project, so I’m not going to figure out how to make it better (I have other stuff to do!) I also found that it is a bit sensitive to the range of girl ages so if this was actual important research paper, this would be of course something I should really think about carefully.
Also here’s a video to show you that you don’t need ChatGPT to make something terrible:
Hiccups and Future Plans
Interestingly, Lou Bega is a German citizen. So this seems all for naught, because really, maybe I should be using the popularity of German names. That’s a big strike. However, this song was inspired by his trip to Florida.
Mambo Number 6 could be the sequel we’re all waiting for. If Mambo Number 6 were released in 2025, what would the names be (similar to the ranking of girls’ names)? That could be a really interesting future project.
Note/Acknowledgement
Also, I’ve decided that I’m going to get back to using my Quarto blog for the write-up, because this is not a great website for data analysis articles. Having to make figures and copy and paste them is frustrating, and the lack of inline LaTeX support is just horrible.
If you find anything wrong (even if it’s minor)… Please, please let me know! Email is damiedpak@gmail.com
I like to thank the lovely Mark J. Rieke for taking a glance at the math as well as my wife.


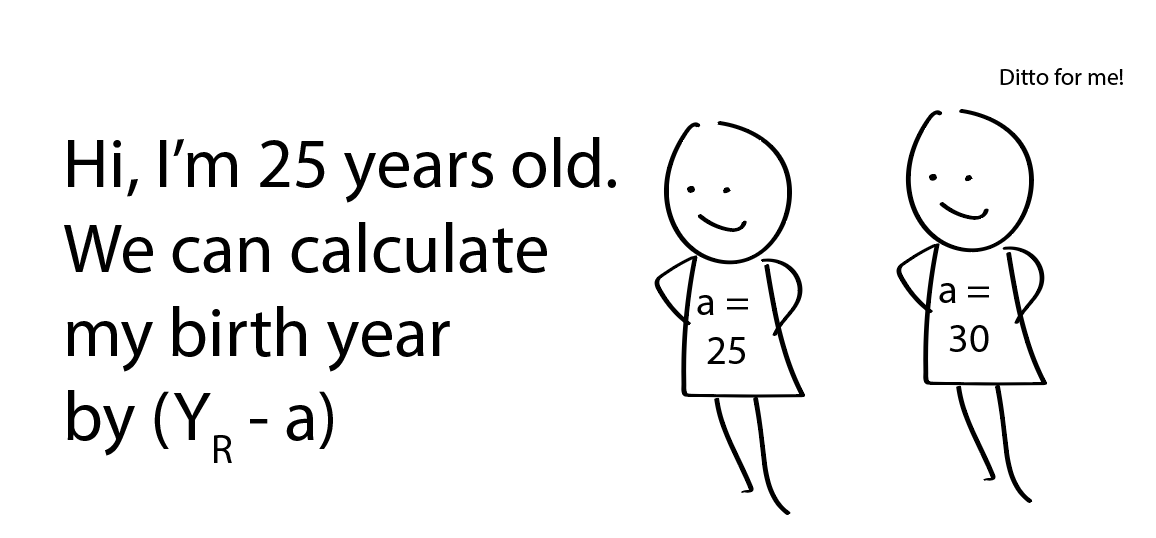

It's interesting how you've applied Bayesian inference to such a playful yet empirical question connecting this analysis of Mambo No. 5 names to your earlier work on uncovering hidden patterns in everday cultural data.
Well done!